Dik ve Özel Üçgenler

• Pisagor, Dünya’nın Güneş etrafında hareket ettiğini keşfetmiştir.
• Pisagor, geometri alanında aksiyomları ve postulatları kullanarak bu alandaki ilk verileri elde etmiştir. Matematik alanına aksiyomatik ve ispat fikrini kazandırmıştır.
• Pisagor, çarpma cetvelini bulmuş ve geometri alanında uygulamıştır.
• Doğadaki her şeyin matematiksel olarak yorumlanabileceğini öne süren Pisagor, aynı zamanda yaşayış ve inanışın da matematik ile yorumlanabileceğini ortaya atmıştır.
• Telin uzunluğuna göre müzik notalarının değişkenlik gösterdiğini ifade etmiş ve notaların sayılarla yorumlanması üzerinde çalışmıştır.
• Pisagor teoremi adı verilen teoremi matematik alanına kazandırmıştır. Pisagor teoreminde rasyonel sayılarla ölçümü yapılamayan uzunlukların var olduğunu ispatlamıştır.

• Pisagor matematik konularını dört gruba ayırmıştır: Soyut sayı bilimi (aritmetik), uygulamalı sayı bilimi (müzik), sükûnet halindeki büyüklükler bilimi (geometri) ve hareket halindeki büyüklükler bilimi (astronomi). Daha sonraları “quadrivium” (dörtlü) denilen bu bilim dalları Avrupa uygarlığında eğitimin temelini teşkil etmiştir. Pisagor’a göre sayılar nesnelerin özüdür. Bu düşünceden özel sayılara ve geometrik şekillere özel nitelikler yükleme düşüncesine geçmiştir. Meselâ aile 3, adalet 4, evlilik 5, canlılık 6, uygun durum ya da zaman 7 sayılarıyla gösterilmiştir. 10 en mükemmel sayıdır; ayrıca çift sayılar dişi, tek sayılar erkektir. Geometrik şekillerden en mükemmel düzlem şekli daire, en mükemmel cisim küredir.

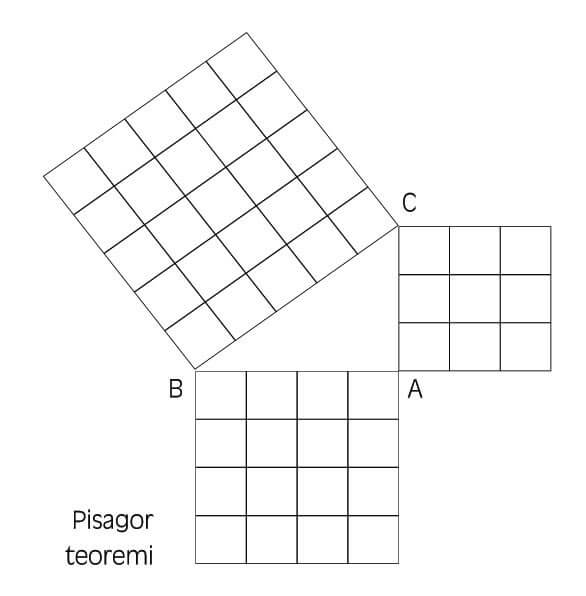
• Pisagor’un matematiğe asıl katkıları geometri alanındadır. Günümüzde kendi adıyla tanınan, dik üçgenlerle ilgili ünlü teoremi o düşünmüş ve kanıtlamıştır. Ancak onun, bir dik üçgende hipotenüs üzerine çizilen karenin alanının iki dik kenar üzerine çizilen karelerin alanları toplamına eşit olduğunu ifade eden bu teoremi (B͞C²=A͞B²+A͞C²) Mısırlılar’dan ve Mezopotamyalılar’dan öğrendikleriyle kurduğu ve kanıtladığı sanılmaktadır.
• Mezopotamya’da bulunan çivi yazılı iki tablet bu olgunun Pisagor’dan en az 1000 yıl önce bilindiğini göstermektedir (Sayılı, s. 195). Ayrıca bir üçgenin iç açıları toplamının 180° tuttuğunu kanıtlayan Pisagor astronomi alanına da büyük bir yenilik getirmiş, dünyanın ve gezegenlerle yıldızların küre şeklinde olduğuna ve dairesel yörüngeler üzerinde hareket ettiğine inandığını açıklamıştır. Onun öğrencisi Filolaos gibi bazıları da dünyayı evrenin merkezine yerleştirmekten vazgeçmiş ve onu gezegen gibi düşünerek hareketli saymışlardır ki bu görüş, XVI. yüzyılda Copernicus’in ortaya koyduğu güneş merkezli evren modelinin ilham kaynağı olmuştur. Pisagor’un görüşleri, tıp alanında evrendeki uyum düşüncesinin insan bedenine uygulanması şeklinde ortaya çıkmıştır. Buna göre bedende yaş ve kuru, sıcak ve soğuk, acı ve tatlı gibi zıt güçlerin dengede olması sağlık durumunu, bu zıtlardan birinin diğerlerinden fazla olması hastalık durumunu gösterir.

Pisagor teoremini ispat etmenin kaç yolu vardır?

• Aşağıdaki video bu güzel teoremin hikayesini ve bir kaç ispatını keyifli bir dil ile anlatıyor. İzlemenizi öneririz. Belki bir gün sizlerde farklı bir ispatını yapmak isteyebilirsiniz, kim bilir?
• Bir daha ki sefere karşınıza bir Pisagor teoremi çıktığında uğruna verilen bunca çabayı hatırlamanız dileğimizle…

ÖKLİD

Grekçe olan adı Eukleides (Euclid, Euclides) İslâm ilim tarihi literatüründe yaygın biçimde Uklîdis, nâdiren de Uklîd imlâsıyla geçmektedir. Müslüman müellifler kendisini geometrinin kurucusu olarak görmüşlerdir. İbnü’n-Nedîm ve İbnü’l-Kıftî, onun günümüzde Lübnan sınırları içinde kalan tarihî Sûr (Tyre) liman şehrinde doğduğunu kaydetmektedir; ancak bu bilgi modern matematik tarihçileri tarafından doğrulanmış değildir. Aynı kaynaklar babasının adını Nûkatares (Naukrates), dedesinin adını Berenîkes (Bereneikes) şeklinde vermektedir. Hayatı hakkındaki yegâne kesin bilgi I. Ptolemaios Soter döneminde (m.ö. 305-283) İskenderiye’de yaşadığı ve matematik öğretmenliği yaptığıdır. Modern araştırmacılara göre Eflâtun’un akademisinde okumuş ve aritmetik, geometri, astronomi, müzik konularına orada ilgi duymaya başlamış olması da muhtemeldir. Eflâtun’un ilk öğrencilerinden sonra ve Archimedes’den önce yıldızının parladığı anlaşılan Öklid’in adı her dönemde ünlü eseri Elementler ile (Gr. Stoikheia, Lat. Elementa, Ar. Kitâbü’l-Erkân, Kitâbü’l-Üsṭuḳussât, Uṣûlü’l-hendese, el-Uṣûl) birlikte anılmıştır.

Daha çok geometri alanında çalışan ve bu alanda yalnız İlkçağ’ın değil neredeyse bütün zamanların en önemli matematikçisi kabul edilen Öklid bilim tarihinde derin bir iz bırakmıştır. Elementler içeriğinden ziyade düzenleniş biçimiyle yeni gelişmeleri etkilemiş, XVIII. yüzyılda gerçekleşen bilimsel devrimin mimarı Isaac Newton’un çalışmalarına esin kaynağı olmuştur. Öklid’in Elementler’de gösterdiği büyük başarı, birkaç temel ilkeden hareketle tümdengelimsel (dedüktif) biçimde zorunlu sonuçların elde edilebildiğini göstermesidir. Eski Grek dünyasında bu yaklaşım doğal olarak geometriye önemli bir niteliğin yüklenmesini sağlamıştır. Öyle ki Grekler geometriyi, bütün gerçekleri açık biçimde öncüllerin kendilerinden çıkan ve asla deneyle kanıtlanmasına gerek bulunmayan önsel (apriori) bilgiler bütünü olarak görmüştür. Öklid geometriye, önermeler arasındaki mantıksal ilişkileri ve ispatlamayı esas alan kuramsal bir bilim kimliği kazandırmış, böylece yeni önermeler veya çözümler bulmak yerine mevcut önerme ve çözümlere mantıksal bir düzen getirmiştir. Bu düzende birkaç öncül ve tanıma dayanarak diğer önermelerin tamamı kanıtlanabilmektedir; tümdengelimsel akıl yürütmeye gücünü veren de bu düzendir.

Öklid, Elementler’de o güne kadar ortaya konulmuş bütün geometri bilgilerini bir araya getirerek sınıflandırmış ve sistemleştirmiştir. Eser aritmetik (sayılar) ve sentetik geometri (nokta, çizgi, düzlem, daire, küre) başta olmak üzere bütün temel matematik konularını içermektedir. Bunları şu şekilde sıralamak mümkündür: I. Kitap: Benzerlik, paraleller, Pisagor teoremi, II. Kitap: Geometrik cebir, yani bugün (a+b)² = a² + 2ab + b² gibi cebirsel ele alınan, o zamanlar geometrik düşünülen özdeşlikler ve alanlar. III. Kitap: Daire ve açı ölçümleri. IV. Kitap: Daire içine ve dışına çokgenlerin çizimi. V. Kitap: Orantı ve cebirsel denklemlerin geometrik çözümü. VI. Kitap: Çokgenlerin benzerliği. VII, VIII ve IX. kitaplar: Aritmetik. X. Kitap: Orantısızlık. XI, XII ve XIII. kitaplar: Uzay geometri.

Aksiyomatik sistem denilen bu konu sıralanışı üç temel unsura dayanmaktadır: Tanımlar, aksiyomlar ve postulatlar. Kitapta nokta, çizgi, yüzey ve cisim gibi geometrik kavramlar tanımlandıktan sonra aksiyomlara geçilmiştir. Aksiyom “doğruluğu herhangi bir kanıt gerektirmeyecek kadar açık ve seçik önerme” demektir. Öklid’in aksiyomları şunlardır: 1. Aynı şeye eşit olan şeyler birbirine de eşittir. 2. Eşit miktarlara eşit miktarlar eklenirse eşitlik bozulmaz. 3. Eşit miktarlardan eşit miktarlar çıkarılırsa eşitlik bozulmaz. 4. Birbiriyle örtüşen şeyler birbirine eşittir. 5. Bütün parçasından büyüktür. Aksiyomlardan sonra postulatlar verilmiştir. Postulat kanıtlanabilir olmasına karşılık kanıtlanmaksızın doğrudan benimsenen önermelerdir. Öklid’in postulatları şunlardır: 1. İki nokta arasını birleştiren en kısa yol doğrudur. 2. Bir doğru doğru olarak sonsuza kadar uzatılabilir. 3. Bir noktaya eşit uzaklıkta bulunan noktaların geometrik yeri çemberdir. 4. Bütün dik açılar birbirine eşittir. 5. İki doğru üçüncü bir doğru tarafından kesilirse iç açılar toplamının 180 dereceden küçük olduğu yönde bu iki doğru kesişir. Bu önermelerden Öklid’in açıkça belirtmediği üç önerme daha çıkarılabilir: 1. Uzay üç boyutludur. 2. Uzay sonsuzdur. 3. Uzay homojendir. Öklid’in paraleller postulatı adıyla tanınan 5. postulatı iyice anlaşılamaması sebebiyle uzun süre teorem olarak kabul edilmiş ve kanıtlanmasına çalışılmıştır. Bazı matematikçiler ise onu değişik biçimlerde ifade etmişlerdir; en tanınmışları şunlardır: 1. Bir üçgenin iç açıları toplamı 180 derecedir. 2. Bir doğruya dışındaki bir noktadan yalnızca bir tek paralel çizilebilir.

• Üçgenler, mimarlık ve mühendislik için en önemli geometrik şekillerden birisidir. Bunun nedeni üçgenlerin dikdörtgen ve karelere oranla daha dayanıklı olması ve şekilleri nedeniyle kolay deforme olmamasıdır.

• Mısır ve dünyanın birçok bölgesinde yapılan piramitlerin günümüze kadar dayanması bu sayededir. Üçgenler sadece mimarlık ve mühendislikte değil spor dallarında da sık karşılaşılan şekillerdir.

Bisikletlerde bir kadro geometrisi vardır ve ilk bakışta iki üçgenin birleşmesinden oluştuğu görülmektedir. Bunun sebebi bisiklet süren kişinin ağırlığı, ayakta pedal çevirip çevirmemesi, bir virajda yatıp yatmaması, zeminin düz olup olmaması durumlarında üzerine yüklenen tüm kuvvetlere en dayanıklı şeklin üçgen olmasıdır.

Bowling oyununda bir top atılarak labutlar devrilmeye çalışılır. Devrilmesi gereken labutların dizilimi üçgen biçimindedir. Bu örnekler artırılabilir.

Üçgen levhalar trafik kuralları ve yollar hakkında bilgi verir. Tehlikeli viraj, yol çalışması, sollama işaretleri buna dâhildir. Tehlikeli durumlar üçgen levhalarla gösterilmektedir.

• Simetrik Eğitim Sistemi (S.E.S) ” adını verdiğimiz konu anlatım tar­zıyla konuların içeriği “Bilgi” kutucuklarına indirgenerek konular sade­leştirilmiştir.
• Verilen bilginin kavratılması amacıyla özgün çözümlü örneklerden oluşan “Bilgi Kavrama” bölümü konulmuştur.
• “Bilgi Kavra­ma” bölümündeki soruların içeriği ile simetrik olacak şekilde seçilmiş olan “Bilgi Uygulama” bölümündeki sorularla, bu bilginin içeriğiyle ilgili olarak bilgi düzeyinizin yükseltilmesi hedeflenmiştir.
• Bölüm sonla­rında bulunan testlerde ise ilgili bölümün tamamını içeren sorular ile bu bölümü tamamen öğrenmenize imkan sağlanmıştır.

• Kahoot aracı her yaştan, herhangi bir dilde, herhangi bir cihazda, herhangi bir konuda öğrenmeyi eğlenceli hale getiren ücretsiz bir oyun tabanlı öğrenme platformudur!
• Yani Kahoot’un öğrenmeyi oyunlaştırarak kolaylaştıran bir platform olduğunu söyleyebiliriz.

Peki  öğrenciler için  neden bu kadar eğlenceli kahoot ?

•         Kendi seçtikleri isimlerle sınava katılıyorlar bu onların  hoşuna gidiyor
•         Sorular sizin belirlediğiniz sürelerde cevaplanmak zorunda bu da işe heyecan katıyor
•         Doğru cevabı kendisinin verdiğini görünce yaşadığı mutluluk , rekabet duygusu
•         Sıkıcı bulduğu ders konuları ile oyun kavramının birlikte olması

Quizizz Nedir?

Quizizz günlük hayatta, işte veya eğitim içerisinde kullandığımız veya gerek duyduğumuz değerlendirme işlemini eğlenceli ve ilgi çekici hale getirmek için oluşturulmuş web platformudur. Katılımcıları gruplar halinde değerlendirmelere katılabilmelerine imkân sağlamaktadır.

Quizizz İle Neler Yapılabilir?

Quizizz ile değerlendirme işlemlerini kolaylaştırmak adına anketler, sınavlar, Quizler oluşturabiliriz. Oluşturduğumuz anketler, sınavlar, quizleri çabucak değerlendirme imkânı sağlayarak sonuçlara çabucak ulaşabiliriz. Sorular içerisinde geri dönütler verebilirsiniz. Değerlendirme işlemleri için belirle zama aralıkları belirleyerek değerlendirme sürecini kontrol edebilirsiniz. Değerlendirme sorularını dilerseniz çıktı olarak çoğaltabilir ve yazılı olarak da uygulayabilirsiniz. Değerlendirme sonuçlarını katılımcıların görüp görmemesi durumlarını kontrol edebilirsiniz.